When landlords of older houses hear the phrase “up to code,” they shudder, because if the City singles them out to pass inspection to make sure their rental property is up to code, it often means some expensive or tedious repairs within a short timeframe. But luckily, good coding doesn’t involve expensive materials or labor (unless you’re hiring someone else to do it), but organization, logic, and attention to detail (and of course, knowledge of the language in which you’re coding). It also helps to use which language is most appropriate for the task. For instance, avoid writing a lot of styles into the HTML–save that for the CSS, which is much more powerful at styling.
Close that tag! You’ll let all the code out!
Always close your tags. This works across several languages, and becomes crucial for html. The notable exception to this, though, is PHP. According to this WordPress PHP guide, it also says to omit the closing PHP tag at the end of the file. This seems counter-intuitive, for one of the main rules is to always close tags, right? The reason not to in this case is that, if your php script has an extra end of line or some whitespace after the closing tag, then that will be spit out in the HTML. The fix? Be sure to remove trailing spaces.
It’s not a big deal, however (so a programmer friend I had to ask about this told me), and if it makes you feel better to close php tags (I have to admit, it does me–though he assured me that php will close its own tags “implicitly” when it sees a new opening php tag, and it will not cause a parse error), then just be scrupulous not to have any trailing spaces. If you are writing php for a header or include file, that means there could be whitespace before PHP sends its HTTP headers, for example if setting a cookie, and that will cause an error. By omitting the closing tag, you never have the chance to make that mistake. (and the mistake, if you make it, is hard to see because it’s just whitespace in the editor)
Besides closing tags, PHP, SQL, and CSS all use semi-colons to close each declaration or property (in fact, a database server won’t know what to do with SQL code until it sees a semi-colon which signals it to execute the code).
What’s in a Name?
Naming–all names in code–variables, classes, etc. should be meaningful enough to be apparent what they do, as well as be lower-case (hyphens seem to be the preferred method of separating words, as later in the css manual, it urges against using underscores, and WordPress discourages the use of camel case altogether). For instance, naming a class in html as “r3-1a” may not be meaningful enough to remember what it pertains to when creating the css rules for it, whereas “company-info” is immediately clear as to what it describes.
Be logical and descriptive, and name things according to purpose, not according to their current appearance (which can change). So, a class of “orange” could at some point change its property to blue. By the same token, it is important in PHP not to truncate variable names so much that you cannot remember what the variable stands for (ie $cpyi instead of $company-info). Naming conventions can make the difference between gibberish and readability.
Sure, the Computer can Read it. But the Question is, Can YOU?
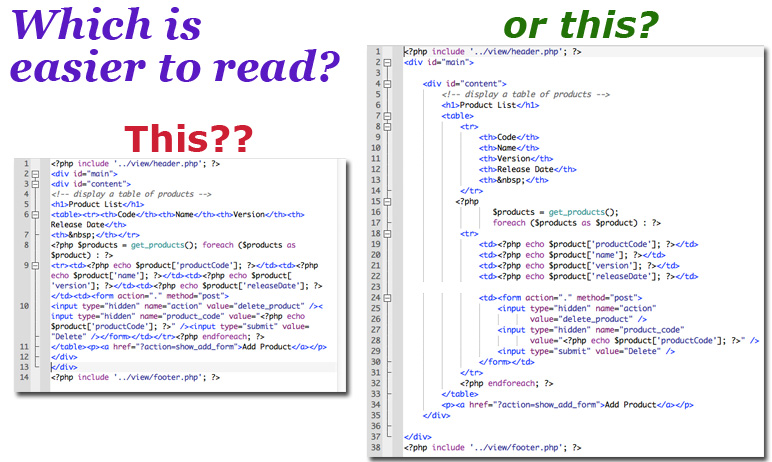
Indentation and line breaks are important for readability of code, especially for figuring out which loop is within which for php. Be sure to have indentation be the same for corresponding blocks. It’s best to use tabs and not spaces to indent (unless it’s the middle of the line, and you want to line up operators). Below is the same code, with indentation and more spacing on the right. Which is easier to read?
“When in doubt, Space it out.”
Space is a good thing, especially as it helps code be more readable. There are several types of “space” in code–actual spaces in the code between operators, indentation (space) to keep blocks of code together and coherent, as well as line spacing between blocks of code. The only space you DON’T want, apparently, is trailing white space, especially in PHP, as mentioned above.
With PHP, always put spaces after commas and on either side of logical, comparison, string, and assignment operators, as well as on both sides of opening and closing parenthesis with if, else if, foreach, for and switch/case blocks. In an array, only put spaces on both side inside of brackets with an actual $variable And with any language, it is important to have space between code blocks, sort of like paragraph spacing, so that the eye does not become overwhelmed and the code is easier to navigate.
Javascript seems spacier than all of the other languages mentioned so far, and the rules put forth by the WordPress handbook on Javascript were so convoluted, I thought it best to just include a screenshot of it below for reference. (If it seems small, click on it for the full size version, which should be more readable.)  This page did add a useful tip that one can find trailing whitespace by enabling visible whitespace characters within your code/text editor.
This page did add a useful tip that one can find trailing whitespace by enabling visible whitespace characters within your code/text editor.
Just as with CSS and PHP, it is best to put Javascript property declarations on separate lines. It is useful to note that all three of these languages also use brackets around their declarations. Use of the semi-colon varies, however. Javascript and SQL have it at the end of each full statement, whereas PHP and CSS use a semi-colon after each property/action.
Validate, validate, validate!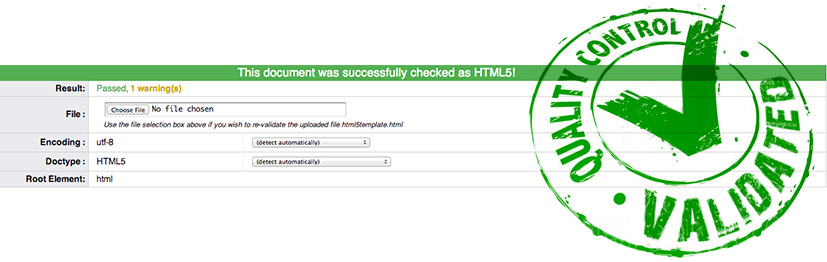
Make sure your HTML validates, as it can help you troubleshoot errors in your code. There are validators for all versions of XML and HTML (though HTML5 is in beta) as well as CSS at w3cschools.org. Not only is this a useful way to find errors in HTML or CSS, I have actually had php files not work because of faulty html (I think I hadn’t closed a form tag). While the validator doesn’t work with files with PHP nested in the html, one way around this is to display the resultant page in a browser which will only render the html, show the source code, copy it, and paste it into the HTML validator on the third tab that says “direct input” to catch possible HTML errors.
Quotation Marks–Remember what you learned in Grade School
With PHP, you can avoid having to escape characters through alternating quoting styles. Also, be sure always to have singe quotes inside of double quotes, just like you did in English Grammar class with quotations.
“She told me ‘Don’t jump!‘ as I was on the ledge,“ Eric said.
php example: echo “<a href=‘$url‘ title=‘url-title‘>$url-title</a>
Also note that with SQL nested in PHP (ie. functions to connect to a database), using quotations correctly is important for the code to work. The grammatical single quotes nested inside of double quotes rule detailed above is a useful analogy. 
While you can get away with being lazy, it’s not a good idea.
Following are a few things that programmers will avoid doing, saying they’re not necessary, as the computer/browser/server can still read the code. Technically, that’s true. But the little extra attention to detail can make code much easier to debug later. After all, it might not be YOU debugging it later–you could do work for a firm that hires someone else behind you to change something, and being lazy with code can put egg on your face later.
Using Braces
It’s good practice to use braces in PHP with if statements, even if there’s only one action, to make it clearer what the action(s) is(are). So, in other words, even when braces are optional, use them anyway. It makes your code far more readable.
Comments
Always always comment your code! That way you’ll be able (or someone else will be able) to find what you’re trying to where more quickly and easily. It can be your way of “bookmarking” your code.
Capitalize Keywords
With SQL by itself (communicating with a database, usually through queries), and SQL statements in PHP, always capitalize the keywords, like UPDATE, INSERT, SELECT, etc, because it makes the code more readable. It also makes the code easier to troubleshoot later, if you get an error, because the keywords will stand out.
It’s also important to note that in most languages used on the web: HTML, CSS, PHP, as well as Javascript, must be coded in lower case to work. SQL is a server-side language, and, depending on what server is being used (I know this is true for MySQL), does not care whether code is upper or lower case.
Organization helps, too.
In CSS, for instance, it is a good idea to have all selectors on one line, or, if you’re using a LOT of selectors (say, for a css reset), then turn on “word wrap” in your text editor so that they’ll display as a big block. It’s good practice to put each property (attribute/value pair) of a selector on a separate line, instead of all on one big line. With CSS, the rule with the most specificity rules, and generally, one starts a CSS file with the broadest, most general rules first, getting more and more specific going down the document (as often later rules that are more specific can then cancel out part of a general rule that went before for just that element). In the WordPress handbook about css coding, it offers a model for ordering the properties within a css rule: 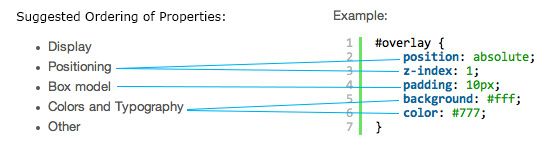
Ordering property declarations alphabetically is another accepted ordering method, and might make it easier to find a specific property inside of a rule. Use whichever logic appeals to you most.
With Vendor prefixes, the preferred order is longest first, ending with the base property being “prefixed” to work in various browsers. (i.e. transition: border-color 0.1s;). A note on spacing in CSS: it is best practice, in property declarations, to follow the colon after the attribute, but to have a space between a number and its measurement (i.e. 24px) will break the CSS code, and it will not register that property. You have been warned.
It is best to plan your html document and corresponding css well in order to be as efficient as possible. Efficiency dictates, for example, not assigning properties to a selector that would normally already have that property (such as all headers are bold, so do not need font-weight: bold, as it’s a given). Some familiarity with default properties of objects, as well as inheritance between objects on a page is invaluable to being efficient. If you assign a font to the body tag, for instance (preferably near the top off your CSS document), then all the headers, paragraph tags, etc, that are “children” of that parent body tag will inherit those attributes. That is why it is more efficient to start out general and work to more specific.
In closing…
Coding comes in time–it just takes lots of practice! Best practices are more suggestions than “rules,” but do help with logic and readability, and it reflects on your work, if you do or do not follow such suggestions. Have fun coding! Just because there are things to keep in mind such as the above, does not mean that you can’t also be creative.
Resources:
HTML validator
http://validator.w3.org/
CSS validator
http://jigsaw.w3.org/css-validator/
WordPress PHP Coding Standards
http://make.wordpress.org/core/handbook/coding-standards/php/
PEAR PHP Coding Standards
http://pear.php.net/manual/en/standards.php
WP HTML Coding Standards
http://make.wordpress.org/core/handbook/coding-standards/html/
WP CSS Coding Standards
http://make.wordpress.org/core/handbook/coding-standards/css/
WP JavaScript Coding Standards
http://make.wordpress.org/core/handbook/coding-standards/javascript/
Connecting to MySQL
http://www.w3schools.com/php/php_mysql_intro.asp